| Class | XII |
| Subject | Mathematics – Eng |
| Chapter | I – Relations and Functions |

























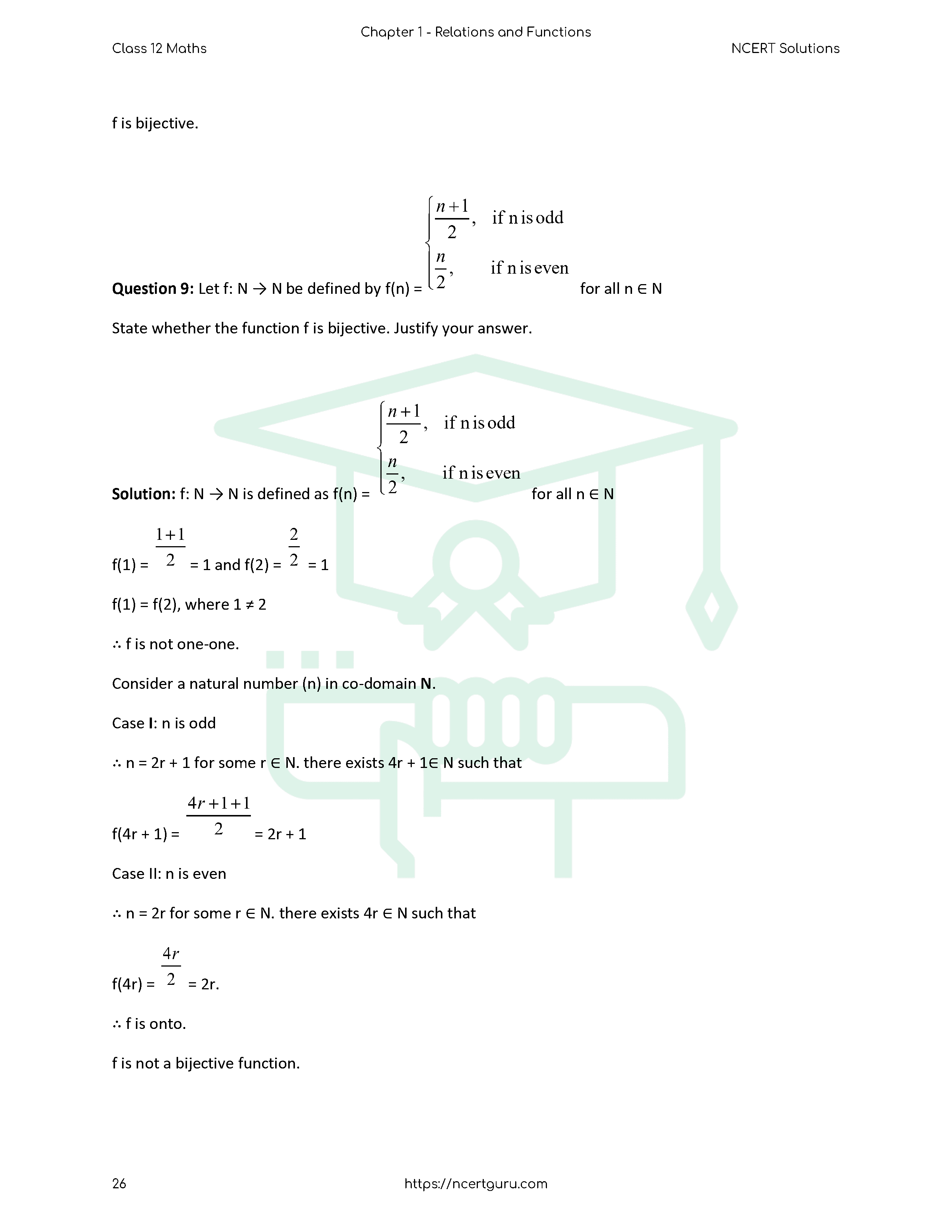













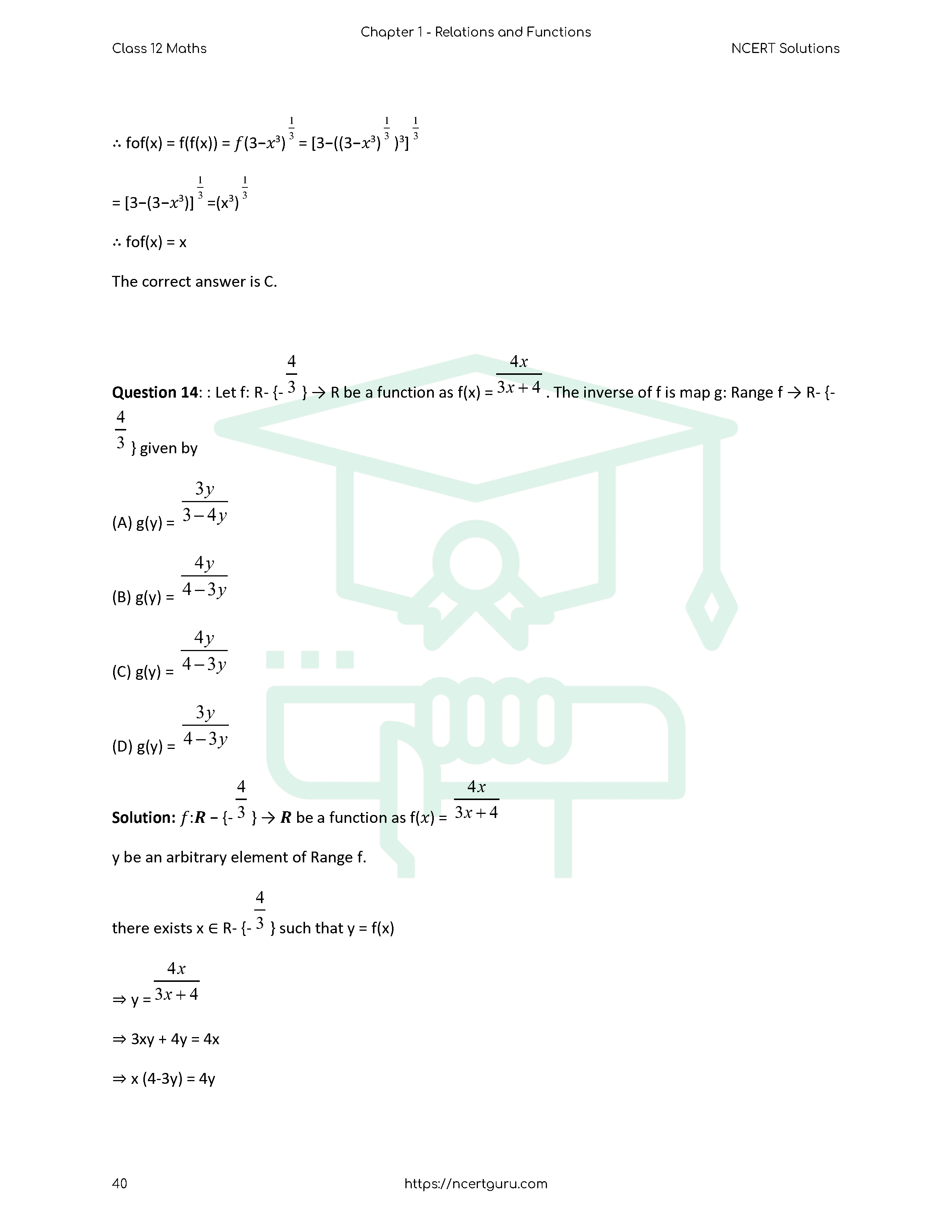
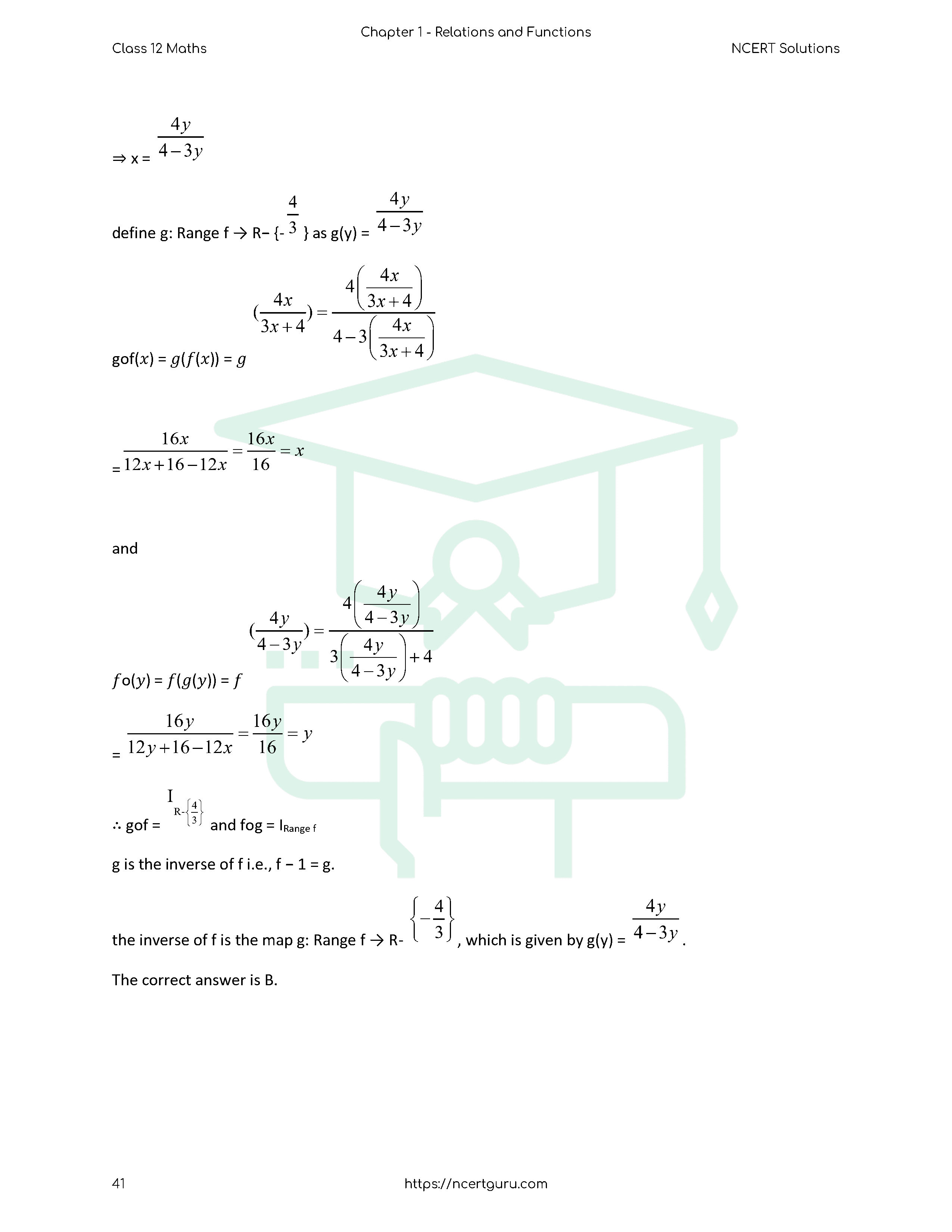















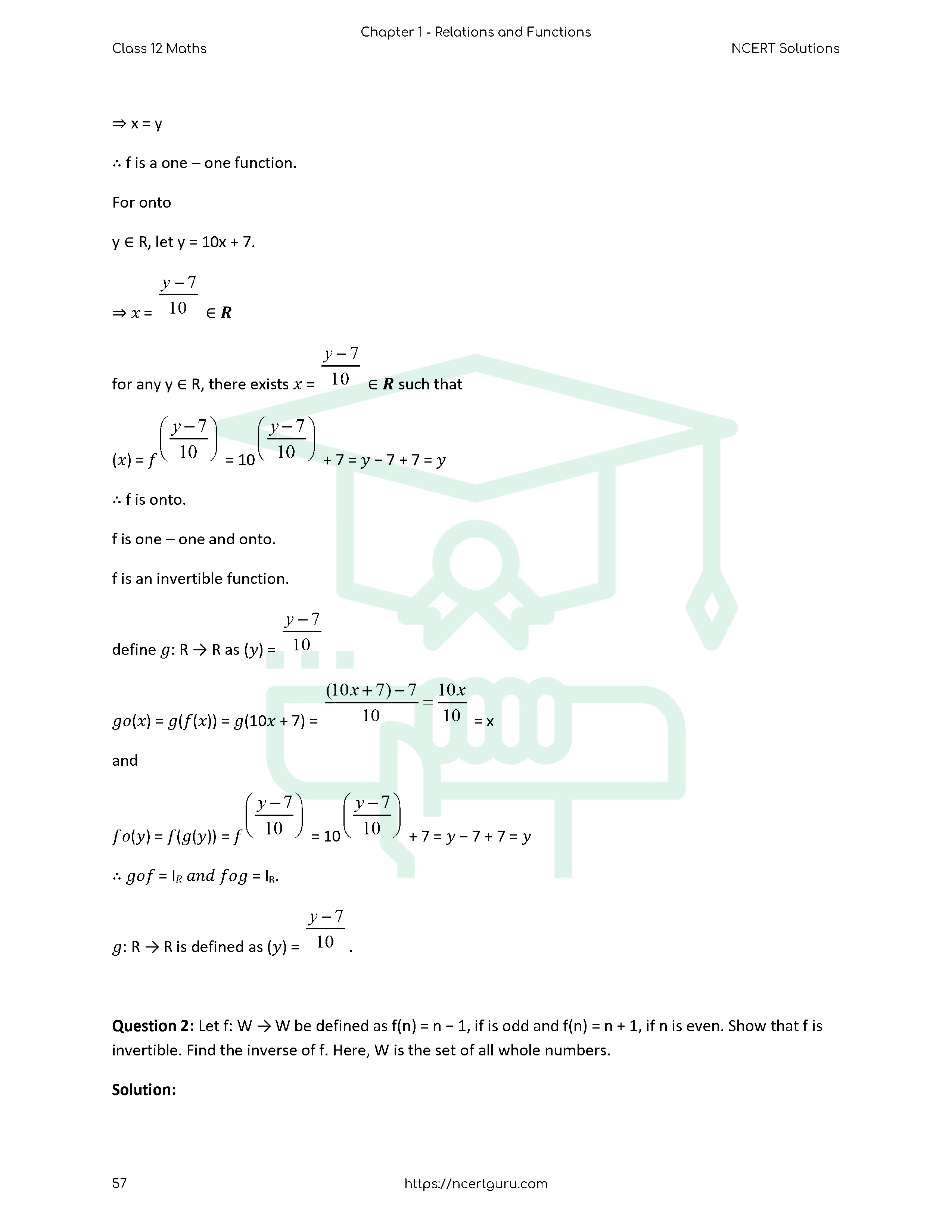













Relations and Functions – Introduction
Students, if you recall that the concept of “Relations and Functions,” “Domain,” “Co-domain,” and “Range” have been introduced in the previous Class XI. Alongside you had also learned various types of real-valued functions and their graph representations.
The term ‘relation’ in mathematics has been taken from the meaning of relationships in the English language, according to those two objects or quantities are related if there are any recognizable connections or links between them.
Suppose ‘A’ set of students of Class XII from a school and ‘B’ set of students of Class XI also from the same school. That means set ‘A’ and set ‘B’ have a connection between them, and that is the same school.
Download NCERT Class 12 Mathematics Books PDF
Types of Relations
In this article, we will discuss a variety of relationships. We know that in a set A, a relationship is a subset of a × A. Hence, the empty set φ ⊂ A × A and A × A themselves are two end relationships.
Definition 1: In set A, a relation R is called a blank relation, if A has no component
A is related to any element i.e. R = φ ⊂ A × A.
Definition 2: In set A, a relationship R is called a universal relationship, if each element of A belongs to each element of A, i.e. R = A × A.
Definition 3: A relation R in a set A is called
- (i) Reflexive, if (a, a) ∈ R, for every a ∈ A,
- (ii) Symmetric, if (a1, a2) ∈ R implies that (a2, a1) ∈ R, for all a1, a2 ∈ A.
- (iii) Transitive, if (a1, a2) ∈ R and (a2, a3) ∈ R implies that (a1, a3) ∈ R, for all a1, a2, a3 ∈ A
Definition 4: In a set A, a relationship R is called an equivalence relationship if R
reflexive, symmetrical, and transitive.
Types of Functions
The concept of function with certain functions such as identification function, stable function, polynomial function, peripheral function, modulus function, sinum function, etc. is given in class XI along with their graphs. The addition, subtraction, multiplication, and division of two tasks have also been studied.
Since the concept of function is of great importance in mathematics and other subjects as well, we would like to expand our study of function from where we had finished earlier. In this part, we would like to study a variety of functions.